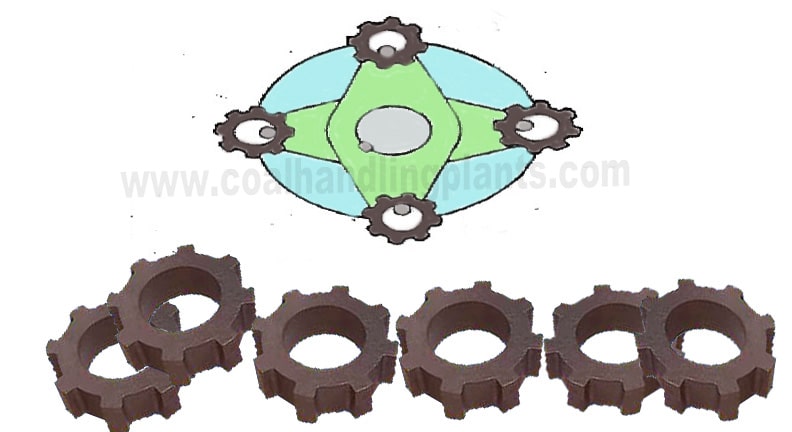
 Example of Ring hammer balancing process –
Example of Ring hammer balancing process –
A granulator has 4 rows of hammer, suppose 2 rows have 18 hammers per row and 2 rows have 20 hammers per rows for a total of 76 hammers per set.
Note – Quantity of hammers and their weight will vary depending upon size of granulator
1. Weight each hammer from a new set individually and accurately. Mark the weight on each hammer. Also list the weights on a sheet of paper.
Suppose the weights of hammers in kg are –
22.50, 22.30, 22.00, 22.10, 22.80, 22.40, 23.00, 22.10, 22.40,23.10, 23.20, 22.50, 22.80, 23.90,23.40, 22.70, 22.40, 22.80, 23.50, 23.60, 22.70, 23.30, 22.60, 22.60, 23.20, 21.20, 22.00, 21.50, 22.40, 22.10, 21.90, 21.60,22.60, 22.00, 23.50, 22.40, 21.80, 21.60, 22.90, 22.50, 23.50, 23.60, 22.50,22.40, 23.00, 22.00, 23.50, 22.60, 22.80, 22.40, 22.40, 22.20, 23.50, 21.90, 22.60, 23.50, 22.70, 23.00, 21.80, 21.20, 21.60, 22.70, 22.70, 22.60, 22.90, 22.80, 22.90, 22.80, 23.00, 22.80, 22.50, 23.20, 23.00, 21.60, 23.5, 23.00
2. Arrange the ring hammer in descending order
23.90, 23.60, 23.60, 23.50, 23.50, 23.50, 23.50, 23.50, 23.50, 23.50, 23.40, 23.30, 23.20, 23.20, 23.20, 23.10, 23.00, 23.00, 23.00, 23.00, 23.00, 23.00, 22.90, 22.90, 22.90, 22.80, 22.80, 22.80, 22.80, 22.80, 22.80, 22.80, 22.70, 22.70, 22.70, 22.70, 22.70, 22.60, 22.60, 22.60, 22.60, 22.60, 22.60, 22.50, 22.50, 22.50, 22.50, 22.50, 22.40, 22.40, 22.40, 22.40, 22.40, 22.40, 22.40, 22.40, 22.30, 22.20, 22.10, 22.10, 22.10, 22.00, 22.00, 22.00, 22.00, 21.90, 21.90, 21.80, 21.80, 21.60, 21.60, 21.60, 21.60, 21.50, 21.20, 21.20
3. On Sheet of paper Make four column A,B,C &D and arrange the ring hammers from maximum weight to minimum weight as mention below and add the weight of each hammer column wise.

4. Opposing rows of hammers ( A and B, C and D must be balanced so that variance in the total weight of each opposing rows of hammers does not exceed the limit value.
5. If the sum of opposite rows of hammers are not equal then interchange the ring hammer of opposite rows in such a way that the the sum of opposite rows should be equal or within limit value.
In fig. 2 we can see that the opposite rows C and D ring hammer weight sum are equal so these opposite rows are balanced. But the total weight sum of opposite rows A and B are not equal so we need to interchange the ring hammer between these opposite rows. The process of interchanging the ring hammer is mention below –
I. Find the average of two opposite unbalance rows.
From fig.2, average weight = (A+B)/2 = (451.5+450.9)/2 = 451.2
II. Find the balancing weight of each unbalance rows
Balancing Weight of row A = row A total weight – average = 451.5 – 451.2 = 0.3 kg
Balancing Weight Of row B = row B total weight – average = 450.9 – 451.2 = – 0.3 kg
III. Interchange the ring hammer of unbalance opposite rows
We have to interchange one or more ring hammer from each unbalance rows in such a way that the difference between two unbalance rows hammer weight is equal or approx to balancing weight and choose heavy weight from the row which have positive balanced weight.
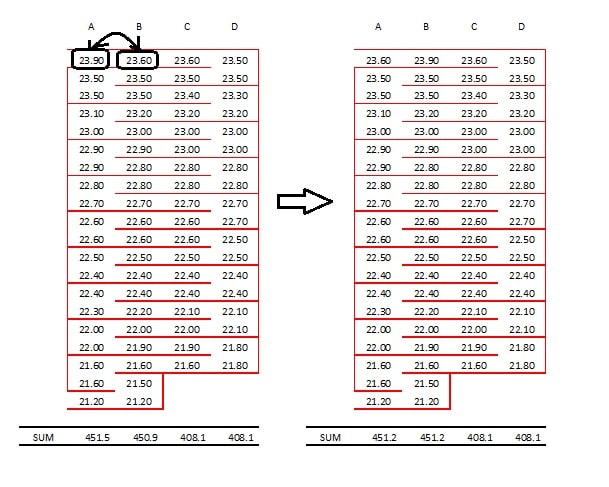
6. After interchanging the weight of unbalanced opposite rows again find the sum of total weight of rows. Finally we get balanced opposite rows.
RELATED SEARCHES: